En esta entrada veremos un ejemplo de distribución de probabilidad de tipo binomial. Recordar que este tipo de distribución es aquella en la que se repite n veces un experimento que tiene una pobabilidad p de éxito y una probabilidad q=1-p de fracaso.
El enunciado del problema es el siguiente:
La probabilidad de que un alumno acabe sus estudios es del 30%. Si en un curso hay 10 alumnos, cual es la probabilidad de que acaben 2 alumnos?
En primer lugar podemos ver que el enunciado nos da una probabilidad de éxito (acabar estudios), una de fracaso (no acabar) y cual es el número de experimentos (alumnos) que se han realizado. Es importante fijarse que todos estos datos nos conducen a la conclusión de que se trata de una distribución binomial. Recordar que en los problemas de distribuciones de probabilidad, en primer lugar es necesario identificar de que tipo se trata. Lo más cómodo, es fijarse en que tipos de datos nos dan y a cual de las distribuciones mejor se ajusta.
El siguiente paso será resolver el problema. Vemos que nos piden cual es la probabilidad de que acaben 2 alumnos, es decir, k=2. Ahora usaremos la expresión de la distribución binomial:
y sustituiremos los valores que nos da el enunciado:
donde p=0,3, q=0,7, n=10 y k=2
Mucho cuidado al realizar la operación, ya que hay muchas posibilidades de equivocarse. Os recomiendo que empecéis por el binomio (os lo hace la calculadora) y después las dos potencias.
O sea, que la probabilidad de que acaben 2 alumnos es del 23%.
Os propongo que sustituyáis p=0,1 n=15 y k=10 y calculéis la nueva probabilidad. Importante también que os cuestionéis el resultado. Tenéis que ser capaces de ver si el resultado es coherente con los datos del enunciado.
Vamos a complicar un poco más el problema. Supongamos que tenemos los mismos datos que el enunciado y nos piden que encontremos la probabilidad de que acaben sus estudios como mucho 3 alumnos. ¿Qué nos quiere decir el enunciado?que acaben 1, 2, 3 o ninguno. Importantísimo ver que ningún alumno puede que no acabe y tiene una probabilidad asociada. ¿Cómo lo resolveremos?
Pues bien, usaremos una ley que nos dice que la probabilidad de la unión de sucesos es la suma de probabilidades, es decir:
P(X<3)=P(0)+P(1)+P(2)+P(3)
siendo cada una de la probabilidades la que encontraremos mediante la fórmula de la distribución binomial. Como podéis comprobar el cálculo es lento y pesado, y es por ello que os animo a que lo hagáis a modo de práctica y igual que os he dicho antes, criticad el resultado y ved si es coherente.
En la próxima entrega dedicada a la probabilidad pondremos un ejemplo de una distribución de Poisson.
Muchas gracias y espero que esta entrada os sea de utilidad.
martes, 30 de octubre de 2012
Efecto inductivo (química orgánica)
El efecto inductivo es el desplazamiento de la carga eléctrica de un enlace simple hacia el átomo o grupo más electronegativo de la molécula.
Según se produzca una cesión o atracción de carga eléctrica, el efecto inductivo se llama +I o -I y viene determinado por el grupo funcional o tipo de molécula. Por ejemplo, los alquilos aumentan el efecto +I (cesión) cuántos más átomos de carbono tengan, es decir, a más carbonos, más aumentará la capacidad de cesión de la carga eléctrica a átomos o grupos más electronegativos.
En la siguiente figura se representan los diferentes átomos y grupos ordenados según su capacidad de cesión o atracción de carga eléctrica, o lo que es lo mismo su efecto inductivo.
Se puede ver que aquellos grupos más electronegativos (capaces de atraer carga eléctrica) son los que poseen un mayor efecto inductivo -I, mientras que los que ceden los electrones son los que tienen efecto +I.
El efecto inductivo tiene gran importancia ya que permiten comprender como van a producirse las reacciones orgánicas según la densidad de carga presente en las moléculas y por tanto saber si éstas serán a tacadas por electrófilos o nucleófilos.
El efecto inductivo nos permite comparar el grado de acidez de distintos compuestos orgánicos. Este ejemplo lo trataremos en una próxima entrada del blog.
Según se produzca una cesión o atracción de carga eléctrica, el efecto inductivo se llama +I o -I y viene determinado por el grupo funcional o tipo de molécula. Por ejemplo, los alquilos aumentan el efecto +I (cesión) cuántos más átomos de carbono tengan, es decir, a más carbonos, más aumentará la capacidad de cesión de la carga eléctrica a átomos o grupos más electronegativos.
En la siguiente figura se representan los diferentes átomos y grupos ordenados según su capacidad de cesión o atracción de carga eléctrica, o lo que es lo mismo su efecto inductivo.
Se puede ver que aquellos grupos más electronegativos (capaces de atraer carga eléctrica) son los que poseen un mayor efecto inductivo -I, mientras que los que ceden los electrones son los que tienen efecto +I.
El efecto inductivo tiene gran importancia ya que permiten comprender como van a producirse las reacciones orgánicas según la densidad de carga presente en las moléculas y por tanto saber si éstas serán a tacadas por electrófilos o nucleófilos.
El efecto inductivo nos permite comparar el grado de acidez de distintos compuestos orgánicos. Este ejemplo lo trataremos en una próxima entrada del blog.
viernes, 26 de octubre de 2012
Ley de Gauss (electromagnetismo) (2)
Esta nueva entrada es la segunda parte de la entrada dedicada la ley de Gauss, que nos permite encontrar el campo eléctrico generado por una distribución continua de carga en cualquier punto del espacio. En la entrada anterior se resolvió el ejemplo de la carga puntual y como encontrar el campo eléctrico generado por esta carga.
Pero si en vez de tener una carga puntual, tratamos de calcular el campo creado por un conductor, tenemos que aplicar aspectos geométricos asociados al conductor. Esta es una de las condiciones para la aplicación de la ley de Gauss, debe existir una ala simetría para su utilización.
Pongamos el ejemplo de una esfera hueca que tiene una densidad superficial de carga. Esto quiere decir que las cargas se distribuyen homogéneamente en la superficie del conductor. Este sería el caso más simple, ya que podemos encontrarnos con distribuciones no homogéneas de carga, pero este aspecto se tratará en entradas posteriores.
Esta densidad superficial de carga se puede expresar como cantidad de carga por unidad de superficie, según la expresión:
siendo S la superficie del conductor.
Vamos a ver un ejemplo de aplicación de la ley de Gauss para un conductor. Se nos pide calcular el campo eléctrico en cualquier punto del espacio creado por una esfera hueca con densidad superficial de carga.
En primer lugar veamos la situación:
Según el dibujo, tenemos un conductor esférico de radio R y se quiere calcular el campo eléctrico creado por este conductor en todo el espacio, es decir para un radio r<R, es decir dentro de la esfera y r>R fuera de la esfera. Recordar que las superficies punteadas son las superficies gaussianas, o sea las superficies que nos permiten encontrar el campo eléctrico.
para r<R:
en la expresión, la parte de la izquierda corresponde a la superficie gaussiana y la parte de la derecha al conductor.
La integral puede simplificarse de la siguiente manera:
esta simplificación siempre es posible, si se conoce la expresión de la superficie escogida. En este caso la superficie es una esfera, de la cual conocemos su expresión de superficie. Sustituimos pues, la expresión de la superficie de la esfera gaussiana.
Ahora analicemos la parte de la derecha de la ley de Gauss, que hace referencia a la carga interior a la superficie gaussiana. Es fácil ver que dentro de la superficie gaussiana para r<R no hay ninguna carga, de manera que es igual a 0 y por tanto:
así pues E=0, no hay campo eléctrico. Es decir, dentro de la esfera hueca con cargas en su superficie no hay ningún campo eléctrico.
para r>R:
la parte de la izquierda de la expresión de mantiene igual, de manera que:
pero la parte derecha cambia, ya que ahora dentro de la superficie gaussiana sí que tenemos carga, que en el fondo es la misma esfera cargada en su superficie.
Pero la carga la podemos expresar en función de la densidad superficial de carga según la expresión que hemos introducido al principio, y nos quedaría:
Pero, esta superficie a quien corresponde? como pertenece a quien tiene la carga, esta superficie es la del conductor, que tiene radio R. La expresión nos queda:
y el campo
como vemos, el campo fuera del conductor depende de su radio, R, y de la distancia al conductor, r.
El procedimiento que hemos visto es el que tenemos que utilizar la ley de Gauss para conductores. Os recomiendamos que sigáis los pasos que hemos explicado. También os recomendamos que intentéis calcular el campo eléctrico creado por un cilindro hueco que tiene densidad superficial de carga.
En la próxima entrada de Gauss resolveremos la esfera maciza.
Espero que os haya sido de utilidad.
Pero si en vez de tener una carga puntual, tratamos de calcular el campo creado por un conductor, tenemos que aplicar aspectos geométricos asociados al conductor. Esta es una de las condiciones para la aplicación de la ley de Gauss, debe existir una ala simetría para su utilización.
Pongamos el ejemplo de una esfera hueca que tiene una densidad superficial de carga. Esto quiere decir que las cargas se distribuyen homogéneamente en la superficie del conductor. Este sería el caso más simple, ya que podemos encontrarnos con distribuciones no homogéneas de carga, pero este aspecto se tratará en entradas posteriores.
Esta densidad superficial de carga se puede expresar como cantidad de carga por unidad de superficie, según la expresión:
siendo S la superficie del conductor.
Vamos a ver un ejemplo de aplicación de la ley de Gauss para un conductor. Se nos pide calcular el campo eléctrico en cualquier punto del espacio creado por una esfera hueca con densidad superficial de carga.
En primer lugar veamos la situación:
Según el dibujo, tenemos un conductor esférico de radio R y se quiere calcular el campo eléctrico creado por este conductor en todo el espacio, es decir para un radio r<R, es decir dentro de la esfera y r>R fuera de la esfera. Recordar que las superficies punteadas son las superficies gaussianas, o sea las superficies que nos permiten encontrar el campo eléctrico.
para r<R:
en la expresión, la parte de la izquierda corresponde a la superficie gaussiana y la parte de la derecha al conductor.
La integral puede simplificarse de la siguiente manera:
esta simplificación siempre es posible, si se conoce la expresión de la superficie escogida. En este caso la superficie es una esfera, de la cual conocemos su expresión de superficie. Sustituimos pues, la expresión de la superficie de la esfera gaussiana.
Ahora analicemos la parte de la derecha de la ley de Gauss, que hace referencia a la carga interior a la superficie gaussiana. Es fácil ver que dentro de la superficie gaussiana para r<R no hay ninguna carga, de manera que es igual a 0 y por tanto:
así pues E=0, no hay campo eléctrico. Es decir, dentro de la esfera hueca con cargas en su superficie no hay ningún campo eléctrico.
para r>R:
la parte de la izquierda de la expresión de mantiene igual, de manera que:
pero la parte derecha cambia, ya que ahora dentro de la superficie gaussiana sí que tenemos carga, que en el fondo es la misma esfera cargada en su superficie.
Pero la carga la podemos expresar en función de la densidad superficial de carga según la expresión que hemos introducido al principio, y nos quedaría:
Pero, esta superficie a quien corresponde? como pertenece a quien tiene la carga, esta superficie es la del conductor, que tiene radio R. La expresión nos queda:
y el campo
como vemos, el campo fuera del conductor depende de su radio, R, y de la distancia al conductor, r.
El procedimiento que hemos visto es el que tenemos que utilizar la ley de Gauss para conductores. Os recomiendamos que sigáis los pasos que hemos explicado. También os recomendamos que intentéis calcular el campo eléctrico creado por un cilindro hueco que tiene densidad superficial de carga.
En la próxima entrada de Gauss resolveremos la esfera maciza.
Espero que os haya sido de utilidad.
jueves, 18 de octubre de 2012
Distribuciones de probabilidad discretas
Hola a tod@s,
En la entrada de hoy hablaremos de las distribuciones de probabilidad discretas. No podremos hacer referencia a todas ellas pero sí a las más importantes.
Recordar que la probabilidad siempre es un valor comprendido entre 0 y 1.
Existen diferentes tipos de funciones de probabilidad discretas, pero las más importantes son las de Bernoulli, Binomial y Poisson.
La función de Bernoulli consiste en realizar un experimento aleatorio una única vez, con p la probabilidad de éxito (que suceda) y 1-p la probabilidad de fracaso (que no suceda).
Si repetimos el experimento n veces tenemos la distribución de probabilidad binomial. En el caso de la distribución binomial los datos a evaluar son: la probabilidad de éxito, p, de fracaso, 1-p y las veces que se repite el experimento, n. La expresión utilizada para calcular la probabilidad de que la variable tome un valor k es:
La última función de distribución discreta es la distribución de Poisson. En esta distribución se dan en sucesos con probabilidades de éxito muy bajas y normalmente en sucesos relacionados con un intervalo de tiempo. Las distribuciones de Poisson se caracterizan por un parámetro que representa el número de veces que ocurre el suceso que estamos estudiando. El cálculo de la probabilidad para una distribución de Poisson es:
Siendo lambda el parámetro característico de la distribució de Poisson.
Hasta aquí hemos hecho un pequeño resumen de las diferentes distribuciones discretas de probabilidad. En próximas entradas introduciremos ejemplos de cada una de las distribuciones.
Espero que os sea de utilidad. Os recomiendo que practiquéis cálculos con números al azar, ya que las fórmulas no son fáciles de aplicar y podéis haceros un pequeño lio al principio.
miércoles, 17 de octubre de 2012
Números cuánticos
Los números cuánticos son unos valores que aparecen al resolver la ecuación de Schrödinger. Recordemos que la ecuación de onda fue postulada por Schrödinger de manera que su solución nos aporte información sobre la posibilidad de encontrar un electrón en una zona concreta alrededor del núcleo atómico.
Estos números cuánticos en un principio eran tres, n, l y m, y con posterioridad se añadió el número cuántico s descubierto por Dirac.
La explicación física más simple que es posible dar de estos números es que se tratan de niveles y subniveles energéticos donde podemos encontrar el electrón. ¿Qué quiere decir esto?Pues bien, que difícilmente podemos imaginarnos como son o que representan físicamente, sólo podemos imaginarlo.
Empezaremos explicando que es cada número cuántico y posteriormente como podemos calcular los números cuánticos correspondiente a un orbital atómico.
El número n o número cuántico principal nos indica el tamaño del orbital y toma valores enteros positivos mayores de 0, es decir, n=1,2,3,4...
El número cuántico l o azimutal indica la forma del orbital que puede ser circular o elíptico y sus valores van de 0 a n-1.
El número cuántico m o magnético indica la orientación del orbital y toma valores de -l a +l.
Pero cuales realmente el significado de los números cuánticos dentro de la estructura electrónica. Pongamos un ejemplo:
Para un electrón con un número cuántico principal 3, los valores de l son 0, 1 y 2, mientras que los valores de m van de -2 a +2. Vamos a anlizar estos valores.
En primer lugar los valores de l, corresponden a los tres tipos de orbitales que podemos encontrar para una n=3, que son s, p y d, es decir cuando l vale 0 estamos en un orbital s. Pero que pasa cuando l vale 2? l=2 representa el orbital p y si a su vez encontramos los valores de m asociados a esta l=1 vemos que son -1, 0 y +1; que curiosamente corresponden a los tres orbitales p (px, py y pz). Y cuales serian los orbitales asociados a l=2?los orbitales d, y cuántos tenemos?cinco que corresponden a los cinco posibles valores de m.
Hagamos un breve resumen del ejemplo antes tratado:
n=3
l=0, 1, 2
m=-2, -1, 0, 1, 2
n=3, l=0 orbitales
n=3, l=1, m=-1, 0, +1 orbitales p
n=3, l=2, m=-2, -1, 0, +1, +2 orbitales d
Ahora nos queda el número cuántico de spin. Este número sólo puede tomar los valores +1/2 y -1/2 y representan el giro del electrón respecto de su eje.
Este número completa la posición de un electrón, veamos:
un orbital s, puede acojer dos electrones, que corresponderán a los dos valores de spin, es decir giros en sentidos opuestos.
Mediante los cuatro números cuánticos podemos ubicar un electrón dentro de su configuración electrónica y como conclusión enunciaremos el principio de exclusión de Pauli. Este principio nos dice que dos electrones no pueden tener los cuatro número cuánticos iguales. Evidentemente, si dos electrones tienen los mismos valores quiere decir que son el mismo electrón, porque ni que sea el número cuántico de spin diferencia dos electrones.
Espero que esta entrada os haya sido de utilidad. Os recomiendo que para afianzar estos conceptos probéis en asignar los números cuánticos a un electrón cualquiera de una configuración electrónica. Podeís probar hacer la configuración de Z=15 y probad a asignar los números cuánticos a cada uno de los electrones que tengáis.
Estos números cuánticos en un principio eran tres, n, l y m, y con posterioridad se añadió el número cuántico s descubierto por Dirac.
La explicación física más simple que es posible dar de estos números es que se tratan de niveles y subniveles energéticos donde podemos encontrar el electrón. ¿Qué quiere decir esto?Pues bien, que difícilmente podemos imaginarnos como son o que representan físicamente, sólo podemos imaginarlo.
Empezaremos explicando que es cada número cuántico y posteriormente como podemos calcular los números cuánticos correspondiente a un orbital atómico.
El número n o número cuántico principal nos indica el tamaño del orbital y toma valores enteros positivos mayores de 0, es decir, n=1,2,3,4...
El número cuántico l o azimutal indica la forma del orbital que puede ser circular o elíptico y sus valores van de 0 a n-1.
El número cuántico m o magnético indica la orientación del orbital y toma valores de -l a +l.
Pero cuales realmente el significado de los números cuánticos dentro de la estructura electrónica. Pongamos un ejemplo:
Para un electrón con un número cuántico principal 3, los valores de l son 0, 1 y 2, mientras que los valores de m van de -2 a +2. Vamos a anlizar estos valores.
En primer lugar los valores de l, corresponden a los tres tipos de orbitales que podemos encontrar para una n=3, que son s, p y d, es decir cuando l vale 0 estamos en un orbital s. Pero que pasa cuando l vale 2? l=2 representa el orbital p y si a su vez encontramos los valores de m asociados a esta l=1 vemos que son -1, 0 y +1; que curiosamente corresponden a los tres orbitales p (px, py y pz). Y cuales serian los orbitales asociados a l=2?los orbitales d, y cuántos tenemos?cinco que corresponden a los cinco posibles valores de m.
Hagamos un breve resumen del ejemplo antes tratado:
n=3
l=0, 1, 2
m=-2, -1, 0, 1, 2
n=3, l=0 orbitales
n=3, l=1, m=-1, 0, +1 orbitales p
n=3, l=2, m=-2, -1, 0, +1, +2 orbitales d
Ahora nos queda el número cuántico de spin. Este número sólo puede tomar los valores +1/2 y -1/2 y representan el giro del electrón respecto de su eje.
Este número completa la posición de un electrón, veamos:
un orbital s, puede acojer dos electrones, que corresponderán a los dos valores de spin, es decir giros en sentidos opuestos.
Mediante los cuatro números cuánticos podemos ubicar un electrón dentro de su configuración electrónica y como conclusión enunciaremos el principio de exclusión de Pauli. Este principio nos dice que dos electrones no pueden tener los cuatro número cuánticos iguales. Evidentemente, si dos electrones tienen los mismos valores quiere decir que son el mismo electrón, porque ni que sea el número cuántico de spin diferencia dos electrones.
Espero que esta entrada os haya sido de utilidad. Os recomiendo que para afianzar estos conceptos probéis en asignar los números cuánticos a un electrón cualquiera de una configuración electrónica. Podeís probar hacer la configuración de Z=15 y probad a asignar los números cuánticos a cada uno de los electrones que tengáis.
martes, 16 de octubre de 2012
Resolución integrales por partes
Uno de los tipos de
integrales que podemos encontrar son las integrales por partes. Estas
integrales consisten normalmente, en el producto de dos funciones que no tienen
ninguna relación o semejanza entre ellas, como por ejemplo el producto de una
función exponencial por una trigonométrica, una trigonométrica por un
polinomio,…
Ésta es la manera más
cómoda de identificar esta clase de integrales, pero, ¿cómo se resuelven? Veamos un ejemplo:
En el ejemplo anterior se resuelve la integral de una función simple como el logaritmo neperiano. De hecho, esta integral está compuesta por dos funciones: el logaritmo y el polinomio que corresponde al número 1, ya que podemos escribir la integral como 1xLn(x).
El resto de integrales por partes sí que están formadas por el producto de dos funciones sin relación.
En otra entrada resolveremos otra integral por parte. De todas formas, esperamos que el video os hay sido de utilidad.
En el ejemplo anterior se resuelve la integral de una función simple como el logaritmo neperiano. De hecho, esta integral está compuesta por dos funciones: el logaritmo y el polinomio que corresponde al número 1, ya que podemos escribir la integral como 1xLn(x).
El resto de integrales por partes sí que están formadas por el producto de dos funciones sin relación.
En otra entrada resolveremos otra integral por parte. De todas formas, esperamos que el video os hay sido de utilidad.
lunes, 15 de octubre de 2012
Ley de Gauss (electromagnetismo)
La ley de Gauss permite el cálculo del campo eléctrico para superficies con alta simetría y nos dice:
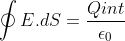
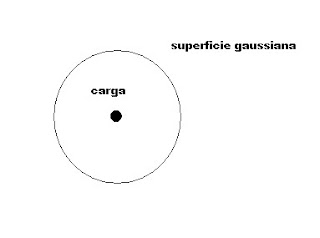
En la figura podemos ver la superficie gaussiana que envuelve a la carga puntual.
Pero ahora, ¿cómo vamos a calcular el campo eléctrico? En primer lugar es importante recordar que el campo eléctrico es un vector y por tanto tiene una dirección. El diferencial de superficie de la fórmula también es un vector. ¿Qué pasa si los vectores son perpendiculares?, que su producto escalar es cero. Es por ello, que es condición indispensable que los vectores E y dS sean paralelos. Recordar que las lineas de campo eléctrico salen de las cargas negativas y van a las positivas, èro en este caso nos es igual el signo de la carga, ya que lo único que nos interesa es su dirección ya que debe ser paralela al dS. ¿Qué pasa con dS? Pues bien, sin entrar en disquisiciones matemáticas, asumiremos que el dS siempre es perpendicular a la superficie que representa.
Como vemos en la imagen el vector de campo eléctrico sale de la carga y es paralelo al vector dS. Pero ahora queda resolver la integral, que como veremos es muy fácil. El por qué es bien simple, si nuestra integral es sobre una curva cerrada para un dS, ¿qué pasa si integramos el dS sobre toda la superficie?, pues que lo que obtenemos es la expresión de la superfície para la geometría que tenemos. En palabras más sencillas, la integral sobre toda la superfície no es más que la fórmula de la superficie de una esfera.
Como vemos, la expresión inicial se ha simplificado mucho, resultando una ecuación con variables conocidas, que son:
E: campo eléctrico
S:superfície de la esfera, que corresponde a la superfície gaussiana elegida, siendo r, el punto donde queremos calcular el campo eléctrico.
La ley de Gauss para este caso queda pues:
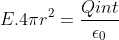
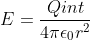
Que es de sobras conocida, ya que es el campo E creado por una carga puntual en cualquier punto del espacio.
Sólo queda explicar cual es el significado de Qint. Representa la carga interior a la superficie gaussiana. Esto quiere decir que si no hay carga dentro de la superficie gaussiana, el campo E es 0. Consejo: dibujad todas las superficies gaussianas posibles que contengan y no la carga o conductor para encontrar el campo en todos los puntos del espacio.
En próximas entradas de nuestro blog, se profundizará tanto en el formalismo matemático que conlleva la ley de Gauss, así como ejemplos más complejos de aplicación de esta misma ley.
¿Qué representa esta
expresión?, nos dice que la integral en una superficie cerrada del campo por
una superficie es igual a la carga interior
partida por la constante dieléctrica.
Vamos a intentar
aclarar qué quiere decir esto. El miembro de la izquierda representa el flujo
de campo eléctrico, que no es más que la cantidad de campo eléctrico que pasa
por unidad de superficie.
En esta explicación
de la ley de Gauss no hemos hecho referencia a todo el formalismo matemático,
ya que esta ley proviene de un teorema matemático mucho más general (teorema de
la divergencia).
El siguiente
concepto que es necesario introducir es el concepto de densidad de carga. Para
entender su significado pensemos en la densidad de un cuerpo, que se define
como la masa por unidad de volumen. Pues bien, en densidad de carga eléctrica
podemos encontrar densidad lineal, superficial y volúmica de carga. Esto quiere
decir que las cargas eléctricas están distribuidas en una recta, en una
superficie y en un volumen.
Vamos a ver un
ejemplo de aplicación de la ley de Gauss. Supongamos que tenemos una carga
eléctrica y queremos calcular el campo eléctrico que genera esta carga en todo
el espacio. Aunque ya conocemos la respuesta por la misma fórmula del campo
eléctrico, usaremos la ley de Gauss.
Si analizamos la ley
de Gauss, el miembro de la izquierda representa la superficie gaussiana sobre
la que calcularemos el campo. Esta superficie la ponemos nosotros y tiene que
ser simétrica para que el campo tenga el mismo valor en cada punto de esta
superficie.
En el caso de una
carga puntual, la superficie gaussiana a escoger será una esfera, ya que en
todos los puntos de su superficie el valor del campo será el mismo.
En la figura podemos ver la superficie gaussiana que envuelve a la carga puntual.
Pero ahora, ¿cómo vamos a calcular el campo eléctrico? En primer lugar es importante recordar que el campo eléctrico es un vector y por tanto tiene una dirección. El diferencial de superficie de la fórmula también es un vector. ¿Qué pasa si los vectores son perpendiculares?, que su producto escalar es cero. Es por ello, que es condición indispensable que los vectores E y dS sean paralelos. Recordar que las lineas de campo eléctrico salen de las cargas negativas y van a las positivas, èro en este caso nos es igual el signo de la carga, ya que lo único que nos interesa es su dirección ya que debe ser paralela al dS. ¿Qué pasa con dS? Pues bien, sin entrar en disquisiciones matemáticas, asumiremos que el dS siempre es perpendicular a la superficie que representa.
Como vemos en la imagen el vector de campo eléctrico sale de la carga y es paralelo al vector dS. Pero ahora queda resolver la integral, que como veremos es muy fácil. El por qué es bien simple, si nuestra integral es sobre una curva cerrada para un dS, ¿qué pasa si integramos el dS sobre toda la superficie?, pues que lo que obtenemos es la expresión de la superfície para la geometría que tenemos. En palabras más sencillas, la integral sobre toda la superfície no es más que la fórmula de la superficie de una esfera.
Como vemos, la expresión inicial se ha simplificado mucho, resultando una ecuación con variables conocidas, que son:
E: campo eléctrico
S:superfície de la esfera, que corresponde a la superfície gaussiana elegida, siendo r, el punto donde queremos calcular el campo eléctrico.
La ley de Gauss para este caso queda pues:
Que es de sobras conocida, ya que es el campo E creado por una carga puntual en cualquier punto del espacio.
Sólo queda explicar cual es el significado de Qint. Representa la carga interior a la superficie gaussiana. Esto quiere decir que si no hay carga dentro de la superficie gaussiana, el campo E es 0. Consejo: dibujad todas las superficies gaussianas posibles que contengan y no la carga o conductor para encontrar el campo en todos los puntos del espacio.
En próximas entradas de nuestro blog, se profundizará tanto en el formalismo matemático que conlleva la ley de Gauss, así como ejemplos más complejos de aplicación de esta misma ley.
Suscribirse a:
Entradas (Atom)